Isabella Garm | 18 Agosto 2023
Para muitos a matemática é fonte de tortura durante os anos de escola, nem todos têm a habilidade para a entender, pois não é simples. No entanto, é uma linguagem fascinante e uma forma interessante de compreender os mistérios do universo.
Este é o caso da sequência de Fibonacci e a sua relação com a proporção áurea. Vamos por partes. A sucessão de Fibonacci é uma série de números que se vão somando de dois em dois, de maneira infinita. Podemos ver assim : 0,1, 1, 2, 3, 5, 8, 13, 21, 34…. Ou seja, obtém-se somando os dois últimos dígitos. Isto é: 0+1=1, 1+1=2, 1+2=3, 2+3=5 e assim consecutivamente.
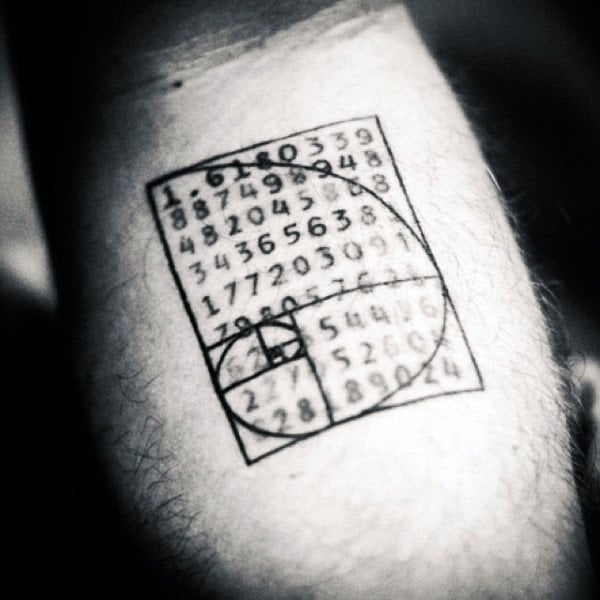
Por outro lado, temos a chamada proporção áurea, também conhecida como divina proporção ou o número de ouro. É um número irracional que expressa a relação entre dois segmentos de uma linha reta. Expressa-se em 1 a 1.618. Esta proporção está associada ao que se considera estético e encontra-se na natureza, na arte e na arquitetura.
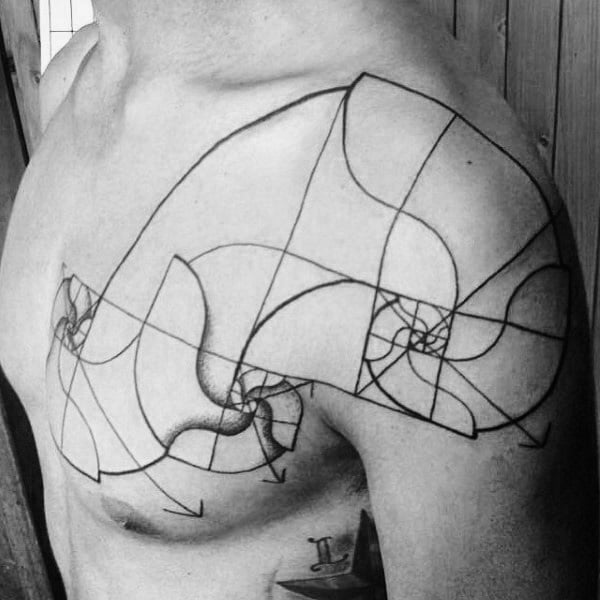
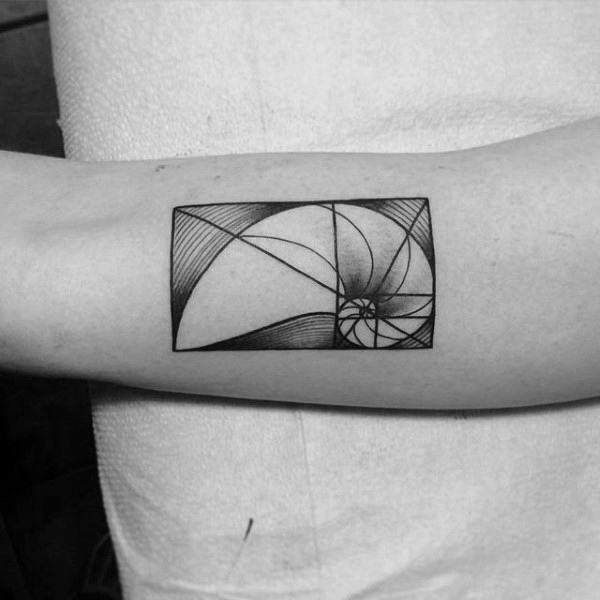
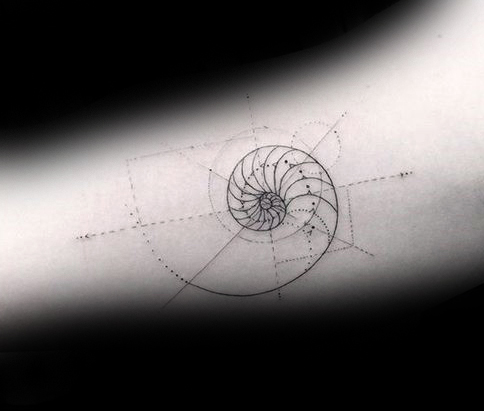
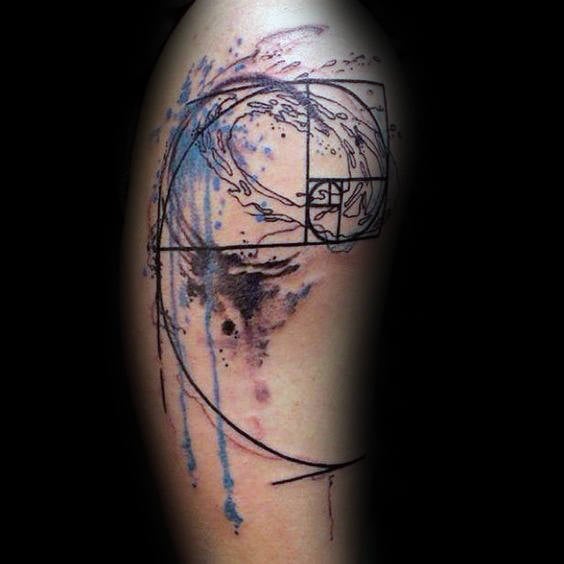
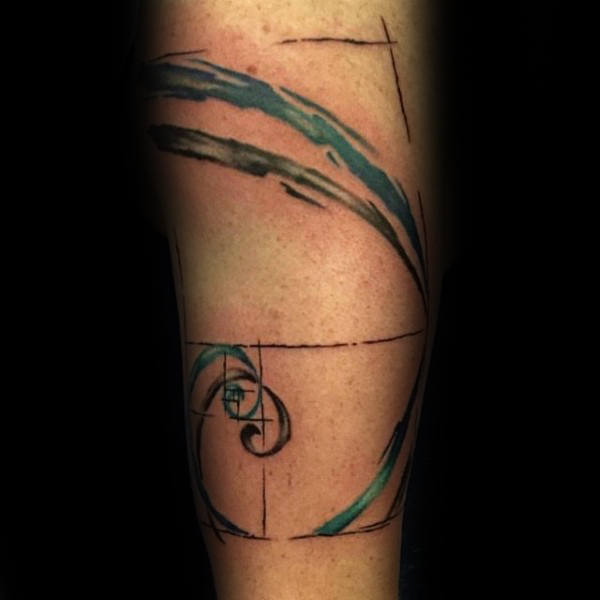
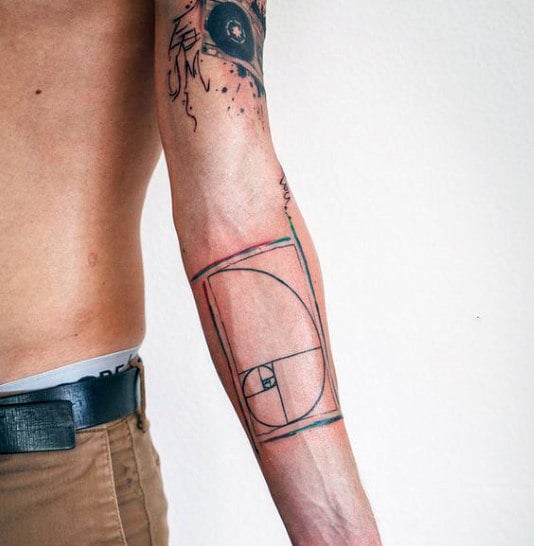
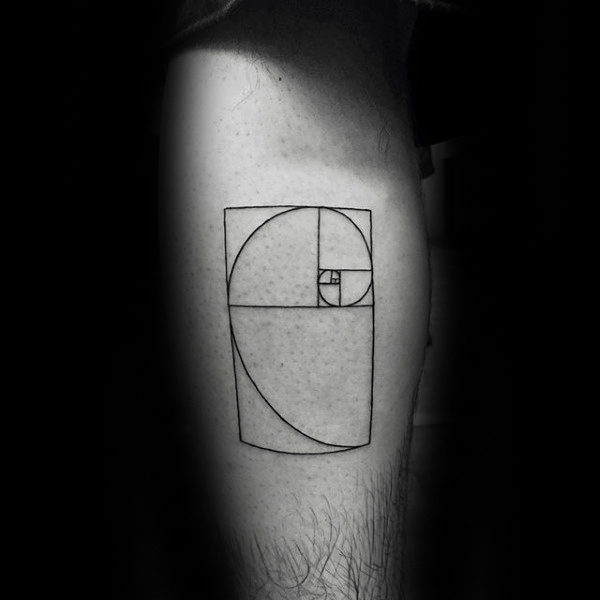
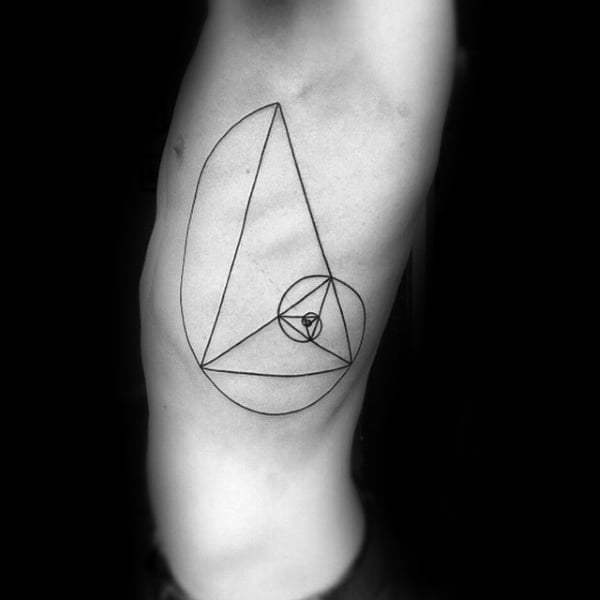
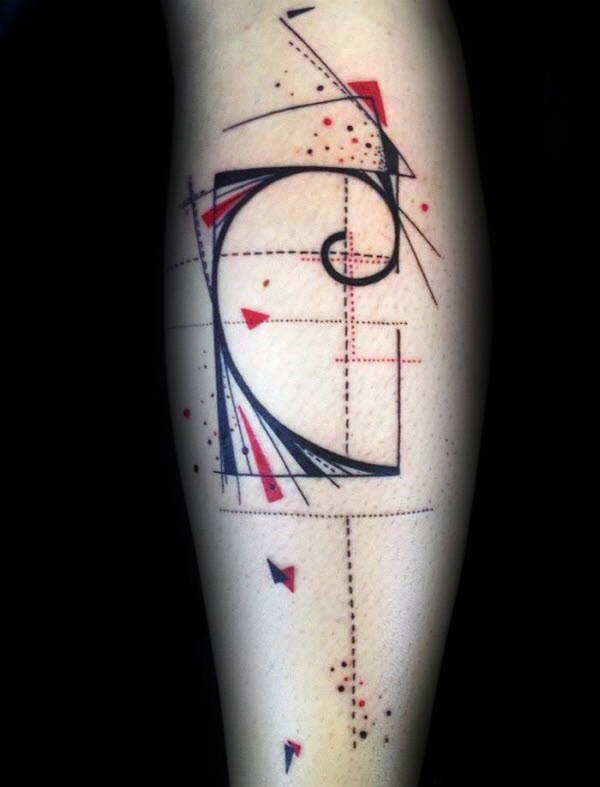
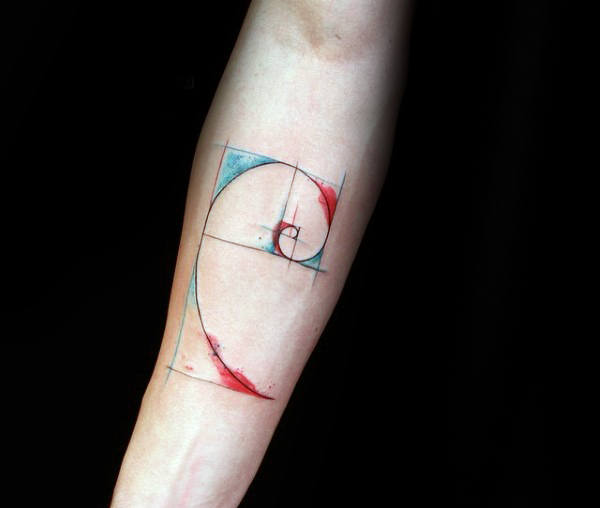
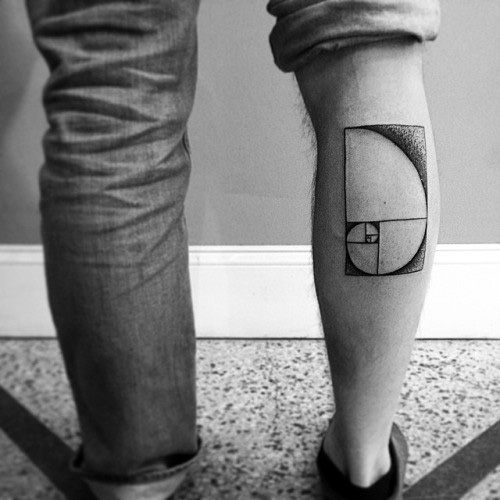
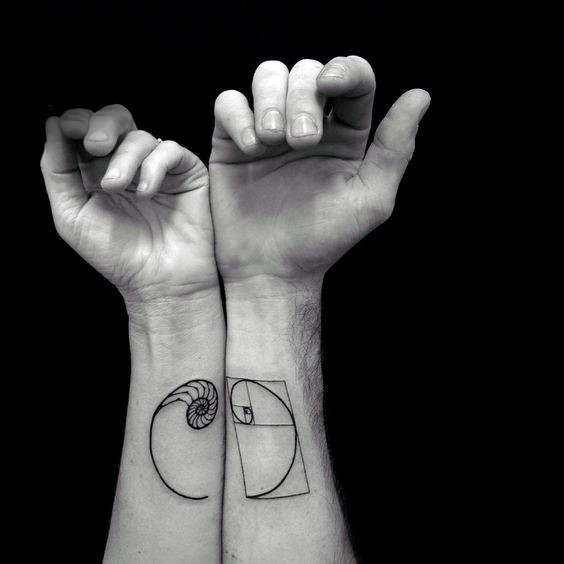
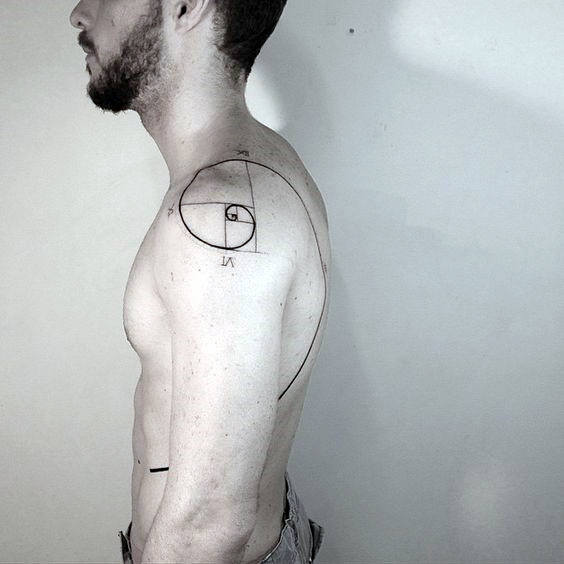
Ambas as expressões matemáticas estão muito conectadas. Uma representação muito conhecida é em espiral. Se se constrói uma figura à base de quadrados, retângulos e curvas que seguem a sequência de Fibonacci, o resultado completo e as suas partes cumprem com a proporção áurea. Literalmente, uma beleza.
A espiral de Fibonacci: Um desenho único
Esta espiral é um desenho muito versátil, precisamente por encontrar-se em diferentes partes do mundo material. Da mesma forma, pode ser representada em vários estilos de tatuagens criando resultados muito impressionantes e chamativos.
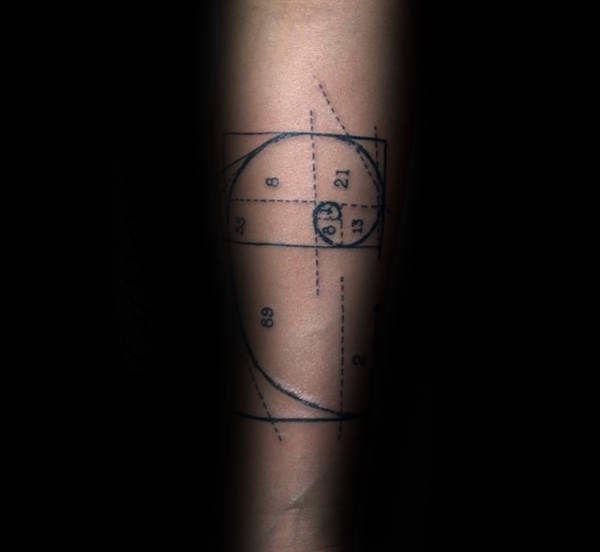
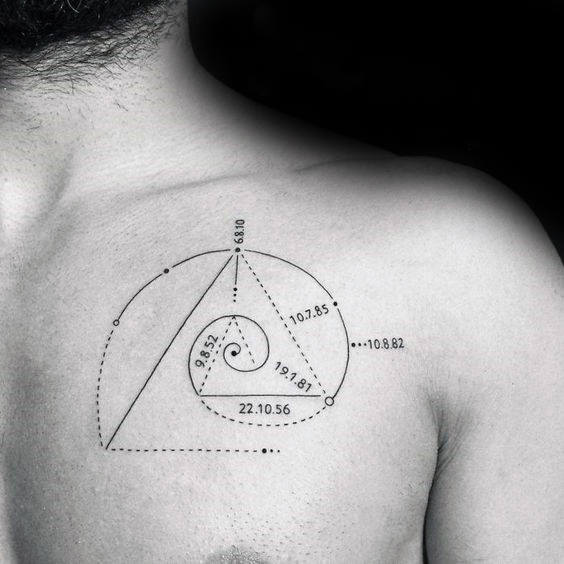
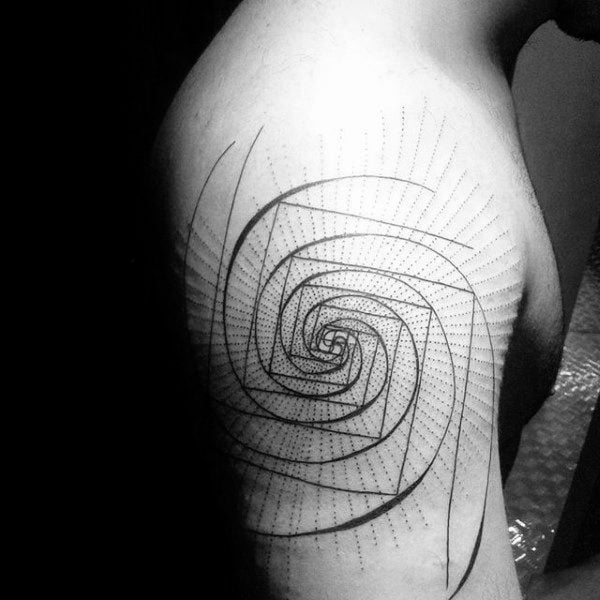
Uma das peças mais populares constitui a espiral mesma, na sua representação de quadros e linhas. Pode ser feito em qualquer tamanho e lugar do corpo. Os estilos minimalista, sketch, geométrico, pontilhismo e blackwork são os mais utilizados para tatuar na pele. Algumas pessoas incluem números, quer sejam os números da proporção áurea ou os dígitos da sequência de Fibonacci.
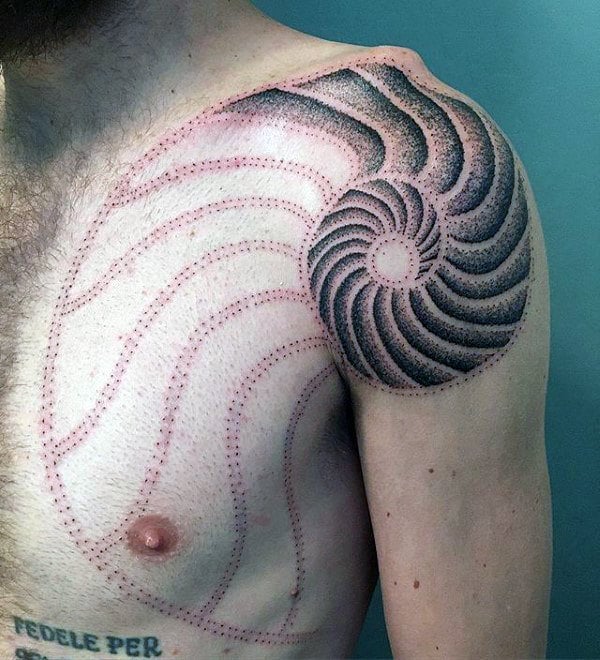
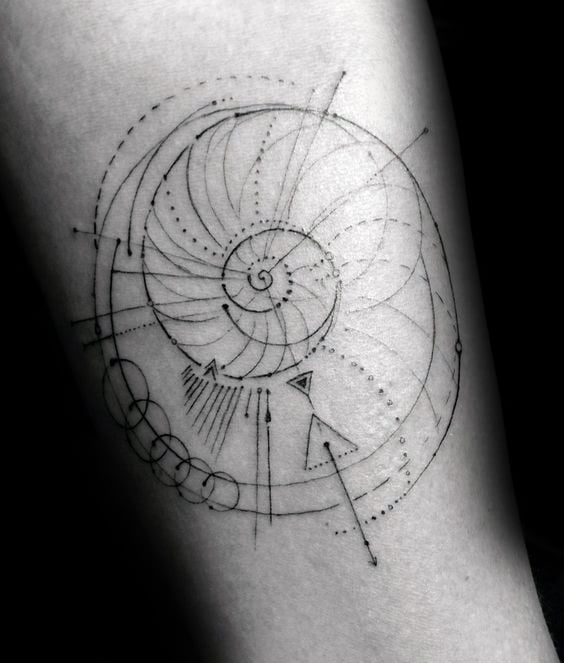
Outra forma muito famosa de mostrar estes princípios matemáticos são as conchas de nautilus, que são muito solicitadas para tatuagens. Além disso, as ondas que podem ter inspiração do Tradicional Japonês, são boas representações da espiral de Fibonacci.
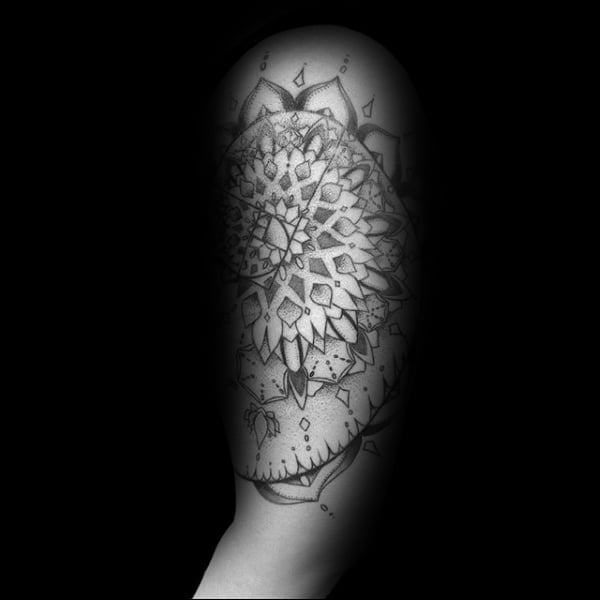
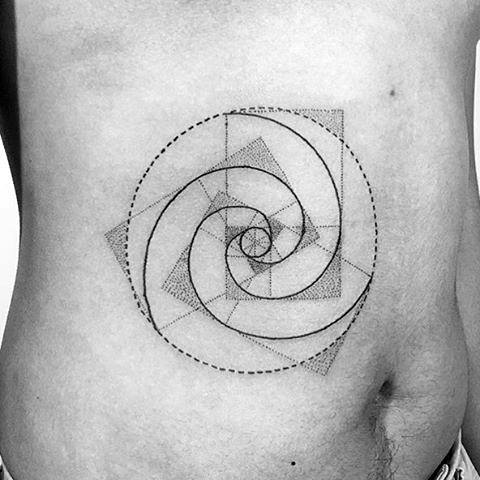
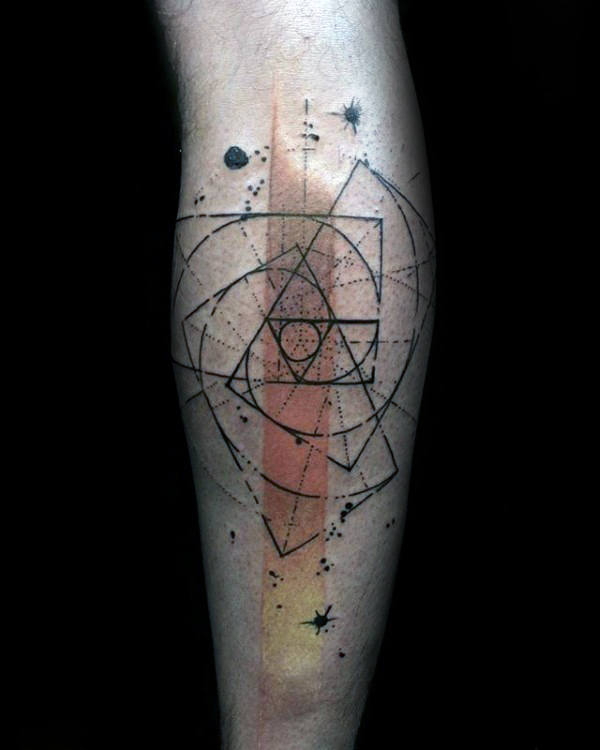
Com esta espiral é possível construir mandalas ou figuras geométricas de diversos níveos de complexidade. Alguns destes desenhos assemelham ou geram ilusões óticas, por isso têm muita dimensão, profundidade e movimento.
Por fim, tem a opção de incorporar a figura espiral a quase qualquer outra imagem. As penas, ramos, bosques ou caveiras destacam-se entre os desenhos mais conhecidos. Este tipo de peças permitem-lhe combinar estilos de tatuagens, sem perder a harmonia do conjunto.
Uma tatuagem ideal para os amantes dos números.
